Menwn : SwkrathV : PaiV MenwnoV : AnutoV
Menon, Sokrates, ein Knabe des Menon, Anytos
SW. Apokrinai toinun palin ex archV:
- ti
fhiV arethn einai kai su kai o etairoV sou;
- was du sagst,
daß die Tugend sei, du und dein Freund!
[13. Menon über Sokrates als verwirrenden Zitterrochen]
MEN. W SwkrateV, hkouon men egwge prin kai suggenesqai [80a] soi
- oti
su ouden allo h autoV te aporeiV kai touV allouV poieiV aporein,
- wste
meston aporiaV gegonenai.
Menon: O Sokrates, ich habe schon gehört, ehe ich noch mit dir (80 a) zusammengekommen bin,
- daß
du allemal nichts als selbst in Verwirrung bist und auch andere in Verwirrung
bringst.
- daß
ich voll Verwirrung geworden bin,
kai dokeiV moi pantelwV, ei dei ti kai skwyai, omoiotatoV einai to te eidoV kai talla tauthi
- thi
plateiai narkhi thi qalattiai.
- kai
su dokeiV moi nun eme toiouton ti pepoihkenai, [narkan]:
und du dünkst mich vollkommen, wenn ich auch etwas scherzen darf, in der Gestalt und auch sonst,
- jenem breiten
Seefisch, dem Zitterrochen, zu gleichen.
- Und so, dünkt
mich, hast auch du mir jetzt etwas Ähnliches angetan, daß ich
erstarre.
alhqwV gar egwge kai [80b] thn yuchn kai to stoma narkw, kai ouk ecw oti apokrinwmai soi.
kaitoi muriakiV ge peri arethV pampollouV logouV eirhka kai proV pollouV,
- kai
panu eu, wV ge emautwi edokoun.
kai moi dokeiV eu bouleuesqai ouk ekplewn enqende oud' apodhmwn.
- ei
gar xenoV en allhi polei toiauta poioiV,
- tac'
an wV gohV apacqeihV.
Denn in der Tat, an Seele (b) und Leib bin ich erstarrt und weiß dir nichts zu antworten;
wiewohl ich schon tausendmal über die Tugend gar vielerlei Reden gehalten habe vor vielen,
- und sehr gut,
wie mich dünkt.
Daher dünkt es mich weißlich gehandelt, daß du von hier mit fortreist, weder zur See noch sonst.
- Denn wenn
du anderwärts dergleichen als Fremder tätest:
- so würde
man dich vielleicht als einen Zauberer abführen.
SW. panourgoV ei, w Menwn, kai oligou exhpathsaV me.
Sokrates: Schlau bist du, Menon, und hättest mich beinahe überlistet.
MEN. ti malista, w SwkrateV;
Menon: Wieso, Sokrates?
[80c] SW. gignwskw ou eneka me hikasaV.
(c) Sokrates: Ich weiß wohl, weshalb du mich so abgebildet hast.
MEN. tinoV dh oiei;
Menon: Weshalb meinst du denn?
SW. ina se anteikasw.
- egw
de touto oida peri pantwn twn kalwn, oti cairousin eikazomenoi
- -
lusitelei gar autoiV. kalai gar oimai twn kalwn kai ai eikoneV -
- all'
ouk anteikasomai se.
- Ich weiß
das von allen Schönen, daß sie gern mögen abgebildet werden.
- Denn es gereicht
ihnen zum Ruhme, weil auch die Bilder der Schönen, meine ich, schön
sind.
- Aber ich werde
dich nicht wieder abbilden.
egw de, ei men h narkh auth narkwsa outw kai touV allouV poiei narkan, eoika authi:
- ei
de mh, ou.
- alla
pantoV mallon autoV aporwn outwV kai touV allouV poiw [80d]
aporein.
- wenn aber
nicht, dann nicht.
- sondern auf
alle Weise bin ich selbst auch in Verwirrung und ziehe nur sodie andern
(d) mit hinein.
kai nun peri arethV o estin egw men ouk oida,
- su
mentoi iswV proteron men hidhsqa prin emou ayasqai,
- nun
mentoi omoioV ei ouk eidoti.
So auch jetzt, was die Tugend ist, weiß ich keineswegs;
- du aber hast
es vielleicht vorher gewußt, ehe du mich berührtest,
- jetzt indes
bist du einem Nichtwissenden ganz ähnlich.
[14. Einwand des Menon: Kann man suchen, was man nicht kennt?]
MEN. kai tina tropon zhthseiV, w SwkrateV, touto
- o
mh oisqa to parapan oti estin;
h ei kai oti malista entucoiV autwi,
- pwV
eishi oti touto estin o su ouk hidhsqa;
- wovon du überhaupt
gar nicht weißt, was es ist?
Oder wenn du es auch noch so gut träfest,
- wie willst
du denn erkennen, daß es dieses ist, was du nicht wußtest?
- oraiV
touton wV eristikon logon katageiV,
oute gar an o ge oiden zhtoi – oiden gar, kai ouden dei twi ge toioutwi zhthsewV-
- -
oute o mh oiden – oude gar oiden oti zhthsei.
- Siehst du,
was für einen streitsüchtigen Satz du uns herbringst?
Nämlich weder was er weiß, kann er suchen, denn er weiß es ja, und es bedarf dafür keines Suchens weiter;
- noch was er
nicht weiß, denn er weiß ja dann auch nicht, was er suchen
soll.
[81a] MEN. oukoun kalwV soi dokei legesqai o logoV outoV, w SwkrateV;
Menon: Scheint dir das nicht ein schöner Satz zu sein, Sokrates? (81 a)
SW. ouk emoige.
Sokrates: Mir gar nicht.
MEN. eceiV legein ophi;
Menon: Kannst du sagen, weshalb?
SW.
egwge:
akhkoa gar andrwn te kai gunaikwn sofwn peri ta qeia pragmata -
Sokrates:
O ja! Denn ich habe es von Männern und Frauen, die in göttlichen
Dingen gar weise waren.
MEN.
tina
logon legontwn;
Menon: Was
sagten denn diese?
SW.
alhqh,
emoige dokein, kai kalon.
Sokrates:
Etwas sehr Wahres, meines Erachtens, und Schönes.
MEN.
tina
touton, kai tineV oi legonteV;
Menon: Aber
was? Und wer waren die, die es sagten?
SW.
oi
men legonteV eisi twn ierewn te kai twn iereiwn osoiV memelhke
- peri
wn metaceirizontai logon oioiV t'
einai [81b]
didonai:
- legei
de kai PindaroV kai alloi polloi twn poihtwn osoi qeioi eisin.
- a
de legousin, tauti estin: alla skopei ei soi dokousin alhqh legein.
- von dem, was
sie verwalten, (b) Rechenschaft geben zu können.
- Es sagt es
auch Pindaros und viele andere Dichter, welche göttlicher Art sind.
- Und was sie
sagen, ist folgendes – erwäge aber wohl, ob dich dünkt, daß
sie wahr reden -:
fasi gar thn yuchn tou anqrwpou einai aqanaton,
- kai
tote men teleutan – o dh apoqnhiskein kalousi -
- tote
de palin gignesqai, apollusqai d'
oudepote:
- so daß
sie zu einer Zeit zwar ende, was man Sterben nennt,
- zu anderer
Zeit jedoch wieder werde, untergehe aber niemals.
dein dh dia tauta wV osiwtata diabiwnai ton bion:
- oisin
gar an -
- Denn von welchen
- Fersefona
poinan palaiou penqeoV
- dexetai,
eiV ton uperqen alion keinwn enatwi etei
- andidoi
yucaV palin,
- [81c]
ek tan basilheV agauoi
- kai
sqenei kraipnoi sofiai te megistoi
- andreV
auxont',
eV de ton loipon cronon hrweV agnoi
- proV
anqrwpwn kaleuntai.
- genommen,
deren Seelen gibt sie der obern Sonne
- im neunten
Jahre zurück,
- (c) aus welchen
dann ruhmvolle tatenreiche
- Könige
und an Weisheit die vorzüglichsten
- Männer
hervorgehn, und von da an als heilige Heroen
- unter den
Menschen genannt werden.
[15. Überwindung des Einwands durch die Lehre der Wiedererinnerung]
ate oun h yuch aqanatoV te ousa kai pollakiV gegonuia,
- kai
ewrakuia kai ta enqade kai ta en aidou kai panta crhmata,
wste ouden qaumaston kai peri arethV kai peri allwn oion t' einai
- authn
anamnhsqhnai, a ge kai proteron hpistato.
- und, was hier
ist und in der Unterwelt, alles erblickt hat:
so daß nicht zu verwundem ist, wenn sie auch von der Tugend und allem andern vermag,
- sich dessen
zu erinnern, was sie ja auch früher gewußt hat.
ouden kwluei en monon anamnhsqenta-
- -o
dh maqhsin kalousin anqrwpoi-
- -talla
panta auton aneurein, ean tiV andreioV hi kai mh apokamnhi zhtwn:
Denn da die ganze (d) Natur unter sich verwandt ist und die Seele alles innegehabt hat:
so hindert nichts, daß, wer nur an ein einziges erinnert wird,
- was bei den
Menschen Lernen heißt,
- alles übrige
selbst auffinde, wenn er nur tapfer ist und nicht ermüdet im Suchen.
oukoun dei peiqesqai toutwi twi eristikwi logwi:
- outoV
men gar an hmaV argouV poihseien
- kai
estin toiV malakoiV twn anqrwpwn hduV akousai,
- wi
egw pisteuwn alhqei einai
- eqelw
meta sou zhtein areth oti estin.
- denn er würde
uns träge machen
- und ist nur
den weichlichen Menschen angenehm zu hören;
- welchem vertrauend,
daß er wahr sei,
- ich eben Lust
habe, mit dir zu untersuchen, was die Tugend ist.
MEN. nai, w Swkrates: alla pwV legeiV touto, oti ou manqanomen,
- alla
hn kaloumen maqhsin anamnhsiV estin;
Menon: Ja, Sokrates, aber meinst du dies so schlechthin, daß wir nicht lernen,
- sondern daß,
was wir so nennen, nur ein Erinnern ist?
SW. kai arti eipon, w Menwn, oti panourgoV ei,
kai [82a] nun erwtaiV ei ecw se didaxai,
- oV
ou fhmi didachn einai all'
anamnhsin,
- ina
dh euquV fainwmai autoV emautwi tanantia legwn.
auch (82 a) jetzt fragst du, ob ich dich lehren kann,
- der ich doch
behaupte, es gebe keine Belehrung, sondern nur Erinnerung,
- damit ich
nur gleich mit mir selbst im Widerspruch erscheine.
MEN. ou ma ton Dia, w SwkrateV, ou proV touto bleyaV eipon, all' upo tou eqouV.
- all'
ei pwV moi eceiV endeixasqai oti ecei wsper legeiV, endeixai.
- Wenn du mir
also irgendwie zeigen kannst, daß es sich so verhält, wie du
sagst, so tue es.
SW. all' esti men ou raidion, omwV de eqelw proqumhqhnai sou eneka.
alla moi proskaleson twn pollwn [82b] akolouqwn toutwni twn sautou ena, ontina boulei,
- ina
en toutwi soi epideixwmai.
Rufe mir also von den vielen Dienern hier, (b) welche dich begleiten, irgendeinen her, welchen du willst,
- damit ich
es dir an diesem zeige.
MEN. panu ge. deuro proselqe.
Menon: Sehr gern. Du da, komm her.
SW. ellhn men esti kai ellhnizei;
Sokrates: Er ist doch ein Hellene und spricht hellenisch?
MEN. panu ge sfodra, oikogenhV ge.
Menon: Sehr gut; er ist im Hause aufgezogen.
SW. prosece dh ton noun opoter' an soi fainhtai,
- h
anamimnhiskomenoV h manqanwn par'
emou.
- ob, als erinnerte
er sich oder als lernte er von nur.
MEN. alla prosexw.
Menon: Das will ich tun.
[16. Beweis dieser Lehre durch Befragung eines Sklaven]
SW. eipe dh moi, w pai, gignwskeiV tetragwnon cwrion oti toiouton estin;
Sokrates: Sage mir also, Knabe, weißt du wohl, daß ein Viereck eine solche Figur ist?
PAIS egwge.
Knabe: Das weiß ich.
SW.
estin
oun [82c]
tetragwnon cwrion isaV econ taV grammaV tautaV pasaV, tettaraV ousaV;
(c) Sokrates:
Gibt es also ein Viereck, welches alle diese Seiten, deren vier sind, gleich
hat?
PAIS
panu
ge.
Knabe: Allerdings.
SW.
ou
kai tautasi taV dia mesou estin isaV econ;
Sokrates:
Hat es nicht auch diese beiden, welche durch die Mitte hindurchgehen, gleich?
PAIS
nai.
Knabe: Ja.
SW.
oukoun
eih an toiouton cwrion kai meizon kai elatton;
Sokrates:
Ein solcher Raum nun kann doch größer und kleiner sein.
PAIS
panu
ge.
Knabe: Freilich.
SW. ei oun eih auth h pleura duoin podoin kai auth duoin,
- poswn
an eih podwn to olon;
- allo
ti apax an hn duoin podoin to cwrion;
- wieviel Fuß
enthielte das Ganze? -
- enthielte
dann nicht der ganze Raum einmal zwei Fuß?
PAIS [82d] nai.
Knabe: Ja.
SW. epeidh de duoin podoin kai tauthi,
- allo
ti h diV duoin gignetai;
- wird er nicht
(d) von zweimal zwei Fuß?
PAIS gignetai.
Knabe: Das wird er.
SW. duoin ara diV gignetai podwn;
Sokrates: Zweimal zwei Fuß ist er also?
PAIS nai.
Knabe: Ja.
SW. posoi oun eisin oi duo diV podeV; logisamenoV eipe.
Sokrates: Wieviel nun zweimal zwei Fuß sind, das rechne aus und sage es.
PAIS tettareV, w SwkrateV.
Knabe: Vier, o Sokrates.
SW. oukoun genoit' an toutou tou cwriou eteron diplasion,
- toiouton
de, isaV econ pasaV taV grammaV wsper touto;
- sonst aber
ein ebensolcher, in dem alle Seiten gleich sind, wie in diesem?
PAIS nai.
Knabe: O ja.
SW.
poswn
oun estai podwn;
Sokrates:
Wieviel Fuß muß er enthalten?
PAIS
oktw.
Knabe: Acht
Fuß.
SW.
fere
dh, peirw moi eipein phlikh tiV estai
[82e]
ekeinou h grammh ekasth.
- h
men gar toude duoin podoin:
Sokrates: Gut! Nun versuche auch, mir zu sagen, wie groß jede Seite in diesem Viereck sein wird.
- Nämlich
die des ersten ist von zwei Fuß;
PAIS dhlon dh, w SwkrateV, oti diplasia.
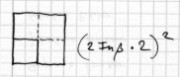
Knabe: Offenbar, o Sokrates, zweimal so groß.
SW. oraiV, w Menwn, wV egw touton ouden didaskw, all' erwtw panta;
kai nun outoV oietai eidenai opoia estin af' hV to oktwpoun cwrion genhsetai:
- h
ou dokei soi;
Und jetzt glaubt er zu wissen, wie groß die Seite ist, aus der das achtfüßige Viereck entstehen wird.
- Oder denkst
du nicht, daß er es glaubt?
MEN. emoige.
Menon: Allerdings.
SW. oiden oun;
Sokrates: Weiß er es aber wohl?
MEN. ou dhta.
Menon: Wohl nicht.
SW. oietai de ge apo thV diplasiaV;
Sokrates: Er glaubt aber doch, es entstehe aus der doppelten?
MEN. nai.
Menon: Ja.
[17. Dessen unvollkommene Lösungsversuche des geometrischen Problems]
SW. qew dh auton anamimnhiskomenon efexhV, wV dei anamimnhiskesqai.
su de moi lege: apo thV diplasiaV grammhV fhiV to [83a] diplasion cwrion gignesqai;
- toionde
legw, mh tauthi men makron, thi de bracu,
- alla
ison pantachi estw wsper touti,
- diplasion
de toutou, oktwpoun:
Sokrates: Sieh nun zu, wie er sich weiter so erinnern wird, wie man sich erinnern muß. -
Du aber sage mir, aus der doppelten Seite, sagst du, entstehe das doppelte Viereck?
- Ich meine
aber ein solches, (83 a) nicht etwa eins, das hier lang ist, dort aber
kurz;
- sondern es
soll nach allen Seiten gleich sein, wie dieses hier,
- aber das Zwiefache
von diesem, also achtfüßig.
PAIS emoige.
Knabe: So meine ich.
SW. oukoun diplasia auth tauthV gignetai,
- an
eteran tosauthn prosqwmen enqende;
- wenn wir hier
noch eine ebenso große hinzusetzen?
PAIS panu ge.
Knabe: Allerdings.
SW. apo tauthV dh, fhiV, estai to oktwpoun cwrion,
- an
tettareV tosautai [83b]
genwntai;
- wenn wir vier
solche nehmen?
PAIS nai.
Knabe: Ja. (b)
SW. anagraywmeqa dh ap' authV isaV tettaraV.
- allo
ti h touti an eih o fhiV to oktwpoun einai;
- Nicht wahr
also, dies wäre, was du für das achtfüßige hältst?
PAIS
panu
ge.
Knabe: Allerdings.
SW.
oukoun
en autwi estin tauti tettara,
- wn
ekaston ison toutwi estin twi tetrapodi;
- deren jedes
diesem Vierfüßigen gleich ist?

PAIS nai.
Knabe:: Ja.
SW. poson oun gignetai; ou tetrakiV tosouton;
Sokrates: Wie groß ist es also? Nicht viermal so groß?
PAIS pwV d' ou;
Knabe: Nicht anders.
SW. diplasion oun estin to tetrakiV tosouton;
Sokrates: Ist nun das viermal so große das zwiefache?
PAIS ou ma Dia.
Knabe: Nein, beim Zeus.
SW. alla posaplasion;
Sokrates: Sondern das wievielfache?

PAIS tetraplasion.
Knabe: Das vierfache.
SW. apo thV diplasiaV [83c] ara, w pai, ou diplasion alla tetraplasion gignetai cwrion.
Sokrates: Aus der zwiefachen Seite also entsteht uns nicht das (c) zwiefache, sondern das vierfache Viereck.
PAIS alhqh legeiV.
Knabe: Du hast recht.
SW. tettarwn gar tetrakiV estin ekkaideka. ouci;
Sokrates: Denn von vier ist das Vierfache sechzehn. Nicht?
PAIS nai.
Knabe: Ja.
SW. oktwpoun d' apo poiaV grammhV;
- ouci
apo men tauthV tetraplasion;
- Nicht wahr,
aus dieser entsteht das vierfache?
PAIS fhmi.
Knabe: Das sage ich auch.
SW. tetrapoun de apo thV hmiseaV tauthsi touti;
Sokrates: Und das vierfüßige entsteht aus dieser halben?
PAIS nai.
Knabe: Ja.
SW. eien: to de oktwpoun ou toude men diplasion estin,
- toutou
de hmisu;
- von diesem
aber die Hälfte?
< PAIS nai.>
Knabe: Allerdings.
SW. ouk apo men meizonoV estai h tosauthV grammhV,
- apo
elattonoV de h [83d]
toshsdi; h ou;
- und aus einer
kleineren als diese? Oder nicht?
PAIS emoige dokei outw.
(d) Knabe: Ich wenigstens denke so.
SW. kalwV:
- to
gar soi dokoun touto apokrinou.
Sokrates: Schön!
- Denn immer
nur, was du denkst, mußt du antworten.
PAIS nai.
Knabe: Ja.
SW. dei ara thn tou oktwpodoV cwriou grammhn meizw men einai thsde thV dipodoV,
- elattw
de thV tetrapodoV.
- und kleiner
als die vierfüßige?
PAIS dei.
Knabe: Das muß sie.
[83e] SW. peirw dh legein phlikhn tina fhiV authn einai.
(e) Sokrates: So versuche denn zu sagen, wie groß du meinst, daß sie sei.
PAIS tripoda.

Knabe: Dreifüßig.
SW. oukoun anper tripouV hi,
- to
hmisu tauthV proslhyomeqa kai estai tripouV;
- kai
enqende wsautwV duo men oide, o de eiV.
Sokrates: Gut. Wenn sie dreifüßig sein soll,
- so wollen
wir von dieser noch die Hälfte dazunehmen, so wird sie dreifüßig;
- und auf dieser
Seite ebenso sind dies zwei, dies einer.
PAIS nai.
Knabe: Ja.
SW. oukoun an hi thide triwn kai thide triwn,
- to
olon cwrion triwn triV podwn gignetai;
- so wird das
ganze Viereck von dreimal drei Fuß.
PAIS fainetai.
Knabe: Offenbar.
SW. treiV de triV posoi eisi podeV;
Sokrates: Dreimal drei aber, wieviel Fuß sind das?

PAIS ennea.
Knabe: Neun.
SW. edei de to diplasion poswn einai podwn;
Sokrates: Wieviel Fuß aber sollte das zwiefache enthalten?
PAIS oktw.
Knabe: Acht.
SW. oud' ar' apo thV tripodoV pw to oktwpoun cwrion gignetai.
Sokrates: Auch nicht aus der dreifüßigen Seite also wird uns das achtfüßige Viereck.
PAIS ou dhta.
Knabe: Freilich nicht.
SW. all' apo poiaV; peirw hmin eipein akribwV:
- kai
[84a]
ei mh boulei ariqmein, alla deixon apo poiaV.
- und wenn du
es nicht durch Zählen willst, so zeige uns (84 a) nur, von welcher.
PAIS alla ma ton Dia, w SwkrateV, egwge ouk oida.
Knabe: Aber beim Zeus, Sokrates, ich weiß es nicht.
[18. Nutzen der im Sklaven erzeugten Verwirrung]
SW. ennoeiV au, w Menwn, ou estin hdh badizwn ode tou anamimnhiskesqai;
oti to men prwton hidei men ou, htiV estin h tou oktwpodoV cwriou grammh,
- wsper
oude nun pw oiden,
- kai
ouc hgeito aporein:
- kai
wsper ouk oiden, oud'
oietai eidenai.
Sokrates: Siehst du wohl, Menon, wie weit er schon fortgeht im Erinnern?
Denn zuerst wußte er zwar auch keineswegs, welches die Seite des achtfüßigen Vierecks ist,
- wie er es
auch jetzt noch nicht weiß:
- und glaubte
nicht, in Verlegenheit zu kommen.
- und wie er
es nicht weiß, so glaubt er es auch nicht zu wissen. (b)
MEN. alhqh legeiV.
Menon:Du hast recht.
SW. oukoun nun beltion ecei peri to pragma o ouk hidei;
Sokrates: Steht es also nun nicht besser mit ihm in Bezug auf die Sache, die er nicht wüßte?
MEN. kai touto moi dokei.
Menon: Auch das dünkt mich.
SW. aporein oun auton poihsanteV kai narkan wsper h narkh,
- mwn
ti eblayamen;
- haben wir
ihm dadurch etwa Schaden getan?
MEN. ouk emoige dokei.
Menon: Mich dünkt nicht.
SW. prourgou goun ti pepoihkamen,
- wV
eoike, proV to exeurein ophi ecei:
tote de raidiwV an kai proV pollouV kai pollakiV [84c] wiet' an
- eu
legein peri tou diplasiou cwriou,
- wV
dei diplasian thn grammhn ecein mhkei.
Sokrates: Vielmehr haben wir vorläufig etwas ausgerichtet, wie es scheint,
- damit er herausfinden
kann, wie sich die Sache verhält.
damals aber glaubte er, ohne Schwierigkeit vor vielen oftmals
- gut zu reden
über das zwiefache Viereck,
- daß
es auch eine zwiefach so lange (c) Seite haben müsse.
MEN. eoiken.
Menon: So mag es wohl sein.
SW. oiei oun an auton proteron epiceirhsai zhtein h manqanein touto
- o
wieto eidenai ouk eidwV,
- prin
eiV aporian katepesen hghsamenoV mh eidenai,
- kai
epoqhsen to eidenai;
- was er nichtwissend
glaubte zu wissen,
- ehe er, überzeugt,
er wisse nicht, in Verwirrung geriet
- und sich nach
dem Wissen sehnte?
MEN. ou moi dokei, w SwkrateV.
Menon: Nein, dünkt mich, Sokrates.
SW. wnhto ara narkhsaV;
Sokrates: Nutzen hat ihm also das Erstarren gebracht?
MEN. dokei moi.
Menon: So dünkt mich.
SW. skeyai dh ek tauthV thV aporiaV oti kai aneurhsei zhtwn met' emou,
- ouden
all'
h erwtwntoV emou kai ou didaskontoV:
- alla
mh taV toutou doxaV anerwtwnta.
Sokrates: Sieh nun aber auch zu, was er von dieser Verlegenheit aus mit mir suchend auch finden wird,
- indem ich
ihn immer nur frage und niemals lehre.
- und nicht
seine eigenen Gedanken nur ihm abfrage.
[19. Sein Finden der Lösung]
lege gar moi su: ou to men tetrapoun touto hmin esti cwrion; manqaneiV;
Sage mir du, ist dies nicht unser vierfüßiges Viereck? Verstehst du?
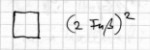
PAIS egwge.
Knabe: Ja.
SW. eteron de autwi prosqeimen an touti ison;
Sokrates: Können wir nun nicht hier noch ein gleiches daran setzen?
PAIS nai.
Knabe: Ja.
SW. kai triton tode ison ekaterwi toutwn;
Sokrates: Und auch dies dritte, das jedem von den beiden gleich ist?
PAIS nai.
Knabe: Ja.
SW. oukoun prosanaplhrwsaimeq' an to en thi gwniai tode;
Sokrates: Können wir nun nicht auch das noch hier in der Ecke ausfüllen?

PAIS panu ge.
Knabe: Allerdings.
SW. allo ti oun genoit' an tettara isa cwria [84e] tade;
Sokrates: Sind dies nun nicht vier gleiche (e) Vierecke?
PAIS nai.
Knabe: Ja.
SW. ti oun; to olon tode posaplasion toude gignetai;
Sokrates: Wie nun? Das wievielfache ist wohl dies Ganze von diesen?
PAIS tetraplasion.
Knabe: Das vierfache.
SW. edei de ge diplasion hmin genesqai: h ou memnhsai;
Sokrates: Wir sollten aber ein zweifaches bekommen; oder erinnerst du dich nicht?
PAIS panu ge.
Knabe: Allerdings.
SW. oukoun estin auth grammh ek gwniaV eiV gwnian [85a]
- [tina]
temnousa dica ekaston toutwn twn cwriwn;
- jedes von
diesen Vierecken in zwei gleiche Teile?
PAIS nai.
Knabe: Ja.
SW. oukoun tettareV autai gignontai grammai isai, periecousai touti to cwrion;
Sokrates: Und werden nicht dieses vier gleiche Linien, welche dieses Viereck einschließen?
PAIS gignontai gar.
Knabe: Allerdings.
SW. skopei dh: phlikon ti estin touto to cwrion;
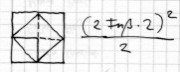
Sokrates: So betrachte nun, wie groß wohl dieses Viereck ist?
PAIS ou manqanw.
Knabe: Das verstehe ich nicht.
SW. ouci tettarwn ontwn toutwn hmisu ekastou ekasth h grammh apotetmhken entoV;
- h
ou;
- Oder nicht?
PAIS nai.
Knabe: Ja.
SW. posa oun thlikauta en toutwi enestin;
Sokrates: Wieviel solche sind nun in diesem?
PAIS tettara.
Knabe: Vier.
SW. posa de en twide;
Sokrates: Wieviel aber in diesem?
PAIS duo.
Knabe: Zwei.
SW. ta de tettara toin duoin ti estin;
Sokrates: Vier aber ist von zwei was doch?
PAIS diplasia.
Knabe: Das Zweifache.
SW. tode oun [85b] posapoun gignetai;
Sokrates: Wievielfüßig (b) ist also dieses?

PAIS oktwpoun.
Knabe: Achtfüßig.
SW. apo poiaV grammhV;
Sokrates: Von welcher Linie?
PAIS apo tauthV.
Knabe: Von dieser.
SW. apo thV ek gwniaV eiV gwnian teinoushV tou tetrapodoV;
Sokrates: Von der, welche aus einem Winkel in den andern das vierfüßige schneidet?
PAIS nai.
Knabe: Ja.
SW. kalousin de ge tauthn diametron oi sofistai:
- wst'
ei tauthi diametroV onoma,
- apo
thV diametrou an, wV su fhiV, w pai MenwnoV,
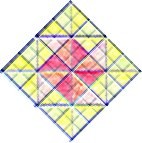
- gignoit'
an to diplasion cwrion.
- so daß,
wenn diese die Diagonale heißt,
- alsdann aus
der Diagonale, wie du behauptest,
- das zwiefache
Viereck entsteht.
PAIS panu men oun, w SwkrateV.
Knabe: Allerdings, Sokrates.
[20. Folgerung: Der Ursprung der Erkenntnis liegt im Lernenden selbst]
SW. ti soi dokei, w Menwn;
estin hntina doxan ouc autou outoV apekrinato;
Sokrates: Was dünkt dich nun, Menon?
Hat dieser irgendeine Vorstellung, die nicht sein war, zur Antwort gegeben?
[85c] MEN. ouk, all' eautou.
(c) Menon: Nein, nur seine eignen.
SW. kai mhn ouk hidei ge, wV efamen oligon proteron.
Sokrates: Und doch wußte er es vor kurzem noch nicht wie wir gestanden?
MEN. alhqh legeiV.
Menon: Ganz recht.
SW. enhsan de ge autwi autai ai doxai: h ou;
Sokrates: Es waren aber doch diese Vorstellungen in ihm. Oder nicht?
MEN. nai.
Menon: Ja.
SW. twi ouk eidoti ara peri wn an mh eidhi eneisin alhqeiV doxai peri toutwn wn ouk oide;
Sokrates: In dem Nichtwissenden also sind von dem, was er nicht weiß, dennoch richtige Vorstellungen.
MEN. fainetai.
Menon: Das zeigt sich.
SW.
kai
nun men ge autwi wsper onar arti anakekinhntai ai doxai autai:
ei
de auton tiV anerhsetai pollakiV ta auta tauta kai pollachi,
- oisq'
oti teleutwn oudenoV htton akribwV
- [85d]
episthsetai peri toutwn.
Wenn ihn aber jemand oftmals um dies nämliche befragt und auf vielfache Art:
- so wisse nur,
daß er am Ende nicht minder genau als irgendein anderer
- um diese Dinge
wissen (d) wird.
MEN. eoiken.
Menon: Das scheint wohl.
SW. oukoun oudenoV didaxantoV all' erwthsantoV
- episthsetai,
analabwn autoV ex autou thn episthmhn;
- wird er wissen
und wird die Erkenntnis nur aus sich selbst hervorgeholt haben?
MEN. nai.
Menon: Ja.
SW. to de analambanein auton en autwi episthmhn ouk anamimnhiskesqai estin;
Sokrates: Dieses nun, selbst aus sich eine Erkennmis hervorholen, heißt das nicht sich erinnern?
MEN. panu ge.
Menon: Allerdings.
SW. ar' oun ou thn episthmhn, hn nun outoV ecei,
- htoi
elaben pote h aei eicen;
- entweder einmal
erlangt oder immer gehabt?
MEN. nai.
Menon: Ja.
SW. oukoun ei men aei eicen, aei kai hn episthmwn:
ei de elaben pote, ouk an en ge twi nun biwi eilhfwV eih.
Sokrates: Hat er sie nun immer gehabt, so ist er auch immer wissend gewesen.
Hat er sie aber einmal erlangt, so hat er sie wenigstens nicht in diesem Leben erlangt.
h [85e] dedidacen tiV touton gewmetrein;
outoV gar poihsei peri pashV gewmetriaV tauta tauta,
- kai
twn allwn maqhmatwn apantwn.
- dikaioV
gar pou ei eidenai, allwV te epeidh en thi shi oikiai gegonen kai teqraptai.
Denn gewiß wird er mit der ganzen Geometrie (e) ebenso verfahren
- und mit allen
andern Wissenschaften auch.
- Denn du mußt
es ja wohl wissen, da er in deinem Hause geboren und erzogen ist.
MEN. all' oida egwge oti oudeiV pwpote edidaxen.
Menon: Ich weiß sehr gut, daß niemand sie ihn jemals gelehrt hat.
SW. ecei de tautaV taV doxaV, h ouci;
Sokrates: Er hat aber diese Vorstellungen; oder nicht?
MEN. anagkh, w SwkrateV, fainetai.
Menon: Notwendig, wie man ja sieht
[21. Rückschluß daraus auf die Unsterblichkeit]
SW. ei de mh en twi nun biwi labwn,
- ouk
hdh touto [86a]
dhlon, oti en allwi tini cronwi eice kai ememaqhkei;
- so hat er
sie ja offenbar in einer andern Zeit gehabt und gelernt. (86a)
MEN. fainetai.
Menon: Offenbar.
SW. oukoun outoV ge estin o cronoV ot' ouk hn anqrwpoV;
Sokrates: Ist nun nicht dieses die Zeit, wo er kein Mensch war?
MEN. nai.
Menon: Offenbar.
SW. ei oun on t' an hi cronon kai on an mh hi anqrwpoV,
- enesontai
autwi alhqeiV doxai,
- ai
erwthsei epegerqeisai episthmai gignontai,
- dhlon
gar oti ton panta cronon estin h ouk estin anqrwpoV.
Sokrates: Wenn also in der ganzen Zeit, wo der Mensch ist, oder auch, wo er es nicht ist,
- richtige Vorstellungen
in ihm sein sollen,
- welche, durch
Fragen aufgeregt, Erkenntnisse werden,
- Denn offenbar
ist er durch alle Zeit entweder Mensch oder nicht.
MEN. fainetai.
Menon: Das ist einleuchtend.
[86b] SW. oukoun ei aei h alhqeia hmin twn ontwn estin en thi yuchi,
- aqanatoV
an h yuch eih,
- -
touto d'
estin o mh memnhmenoV -
- epiceirein
zhtein kai anamimnhiskesqai;
Sokrates: Wenn nun von jeher immer die Wahrheit von allem, (b) was ist, der Seele einwohnt,
- so wäre
ja die Seele unsterblich,
- das heißt
aber, dessen du dich nicht erinnerst,
- trachten kannst
zu suchen und dir zurückzurufen.
MEN. eu moi dokeiV legein, w SwkrateV, ouk oid' opwV.
Menon: Du scheinst mir, ich weiß nicht wie, vortrefflich zu reden, Sokrates.
SW. kai gar egw emoi, w Menwn.
- kai
ta men ge alla ouk an panu uper tou logou diiscurisaimhn:
- beltiouV
an eimen kai andrikwteroi kai htton argoi
- mhde
dein zhtein,
Sokrates: Auch mir selbst scheine ich es, o Menon.
- Und das Übrige
freilich möchte ich nicht eben ganz verfechten für diese Rede;
- besser werden
und mannhafter und weniger träge, (c)
- und man müsse
es also auch nicht erst suchen,
MEN. kai touto men ge dokeiV moi eu legein, w SwkrateV.
Menon: Auch dies dünkt mich sehr richtig gesagt, Sokrates.
SW. boulei oun, epeidh omonooumen oti zhthteon peri ou mh tiV oiden,
- epiceirhswmen
koinhi zhtein ti pot'
estin areth;
- willst du,
daß wir miteinander unternehmen zu suchen, was wohl die Tugend ist?