Menôn : Sôkratês : Pais Menônos : Anutos
Menon, Sokrates, ein Knabe des Menon, Anytos
SÔ. apokrinai toinun palin ex archês:
- ti phêis
aretên einai kai su kai ho hetairos sou?
Sokrates: Antworte also nochmals von vorne,
- was du sagst,
daß die Tugend sei, du und dein Freund!
[13. Menon über Sokrates als verwirrenden Zitterrochen]
MEN. ô Sôkrates, êkouon men egôge prin kai sungenesthai [80a] soi
- hoti su ouden
allo ê autos te aporeis kai tous allous poieis aporein,
- hôste
meston aporias gegonenai.
Menon: o Sokrates, ich habe schon gehört, ehe ich noch mit dir (80 a) zusammengekommen bin,
- daß
du allemal nichts als selbst in Verwirrung bist und auch andere in Verwirrung
bringst.
- daß
ich voll Verwirrung geworden bin,
kai dokeis moi pantelôs, ei dei ti kai skôpsai, homoiotatos einai to te eidos kai t'alla tautêi
- têi
plateiai narkêi têi thalattiai.
- kai su dokeis
moi nun eme toiouton ti pepoiêkenai [narkan]:
und du dünkst mich vollkommen, wenn ich auch etwas scherzen darf, in der Gestalt und auch sonst,
- jenem breiten
Seefisch, dem Zitterrochen, zu gleichen.
- Und so, dünkt
mich, hast auch du mir jetzt etwas Ähnliches angetan, daß ich
erstarre.
alêthôs gar egôge kai [80b] tên psuchên kai to stoma narkô, kai ouk echô hoti apokrinômai soi.
kaitoi muriakis ge peri aretês pampollous logous eirêka kai pros pollous,
- kai panu eu,
hôs ge emautôi edokoun.
kai moi dokeis eu bouleuesthai ouk ekpleôn enthende oud' apodêmôn.
- ei gar xenos
en allêi polei toiauta poiois,
- tach' an hôs
goês apachtheiês.
Denn in der Tat, an Seele (b) und Leib bin ich erstarrt und weiß dir nichts zu antworten;
wiewohl ich schon tausendmal über die Tugend gar vielerlei Reden gehalten habe vor vielen,
- und sehr gut,
wie mich dünkt.
Daher dünkt es mich weißlich gehandelt, daß du von hier mit fortreist, weder zur See noch sonst.
- Denn wenn
du anderwärts dergleichen als Fremder tätest:
- so würde
man dich vielleicht als einen Zauberer abführen.
SÔ. panourgos ei, ô Menôn, kai oligou exêpatêsas me.
Sokrates: Schlau bist du, Menon, und hättest mich beinahe überlistet.
MEN. ti malista, ô Sôkrates?
Menon: Wieso, Sokrates?
[80c] SÔ. gignôskô hou heneka me êikasas.
(c) Sokrates: Ich weiß wohl, weshalb du mich so abgebildet hast.
MEN. tinos dê oiei?
Menon: Weshalb meinst du denn?
SÔ. hina se anteikasô.
- egô
de touto oida peri pantôn tôn kalôn, hoti chairousin
eikazomenoi
- - lusitelei
gar autois. kalai gar oimai tôn kalôn kai hai eikones -
- all' ouk anteikasomai
se.
Sokrates: Damit ich dich wieder abbilden möchte.
- Ich weiß
das von allen Schönen, daß sie gern mögen abgebildet werden.
- Denn es gereicht
ihnen zum Ruhme, weil auch die Bilder der Schönen, meine ich, schön
sind.
- Aber ich werde
dich nicht wieder abbilden.
egô de, ei men hê narkê autê narkôsa houtô kai tous allous poiei narkan, eoika autêi:
- ei de mê,
ou.
- alla pantos
mallon autos aporôn houtôs kai tous allous poiô [80d]
aporein.
Ist nun dein Zitterrochen selbst auch erstarrt, wenn er andere erstarren macht, dann gleiche ich ihm;
- wenn aber
nicht, dann nicht.
- sondern auf
alle Weise bin ich selbst auch in Verwirrung und ziehe nur sodie andern
(d) mit hinein.
kai nun peri aretês ho estin egô men ouk oida,
- su mentoi
isôs proteron men êidêstha prin emou apsasthai,
- nun mentoi
homoios ei ouk eidoti.
So auch jetzt, was die Tugend ist, weiß ich keineswegs;
- du aber hast
es vielleicht vorher gewußt, ehe du mich berührtest,
- jetzt indes
bist du einem Nichtwissenden ganz ähnlich.
[14. Einwand des Menon: Kann man suchen, was man nicht kennt?]
MEN. kai tina tropon zêtêseis, ô Sôkrates, touto
- ho mê
oistha to parapan hoti estin?
ê ei kai hoti malista entuchois autôi,
- pôs
eisêi hoti touto estin ho su ouk êidêstha?
Menon: Und auf welche Weise willst du denn dasjenige suchen, Sokrates,
- wovon du überhaupt
gar nicht weißt, was es ist?
Oder wenn du es auch noch so gut träfest,
- wie willst
du denn erkennen, daß es dieses ist, was du nicht wußtest?
- horais
touton hôs eristikon logon katageis,
oute gar an ho ge oiden zêtoi – oiden gar, kai ouden dei tôi ge toioutôi zêtêseôs –
- – oute
ho mê oiden – oude gar oiden hoti zêtêsei.
Sokrates: Ich verstehe, was du sagen willst, Menon!
- Siehst du,
was für einen streitsüchtigen Satz du uns herbringst?
Nämlich weder was er weiß, kann er suchen, denn er weiß es ja, und es bedarf dafür keines Suchens weiter;
- noch was er
nicht weiß, denn er weiß ja dann auch nicht, was er suchen
soll.
[81a] MEN. oukoun kalôs soi dokei legesthai ho logos houtos, ô Sôkrates?
Menon: Scheint dir das nicht ein schöner Satz zu sein, Sokrates? (81 a)
SÔ. ouk emoige.
Sokrates: Mir gar nicht.
MEN. echeis legein hopêi?
Menon: Kannst du sagen, weshalb?
SÔ. egôge:
akêkoa gar andrôn te kai gunaikôn sophôn peri ta
theia pragmata –
Sokrates:
O ja! Denn ich habe es von Männern und Frauen, die in göttlichen
Dingen gar weise waren.
MEN. tina
logon legontôn?
Menon: Was
sagten denn diese?
SÔ.
alêthê, emoige dokein, kai kalon.
Sokrates:
Etwas sehr Wahres, meines Erachtens, und Schönes.
MEN. tina
touton, kai tines hoi legontes?
Menon: Aber
was? Und wer waren die, die es sagten?
SÔ.
hoi men legontes eisi tôn hiereôn te kai tôn hiereiôn
hosois memelêke
- peri hôn
metacheirizontai logon hoiois t' einai [81b] didonai:
- legei de kai
Pindaros kai alloi polloi tôn poiêtôn hosoi theioi eisin.
- ha de legousin,
tauti estin: alla skopei ei soi dokousin alêthê legein.
Sokrates: Die es sagen, sind Priester und Priesterinnen, so viele es deren gibt, denen daran gelegen ist,
- von dem, was
sie verwalten, (b) Rechenschaft geben zu können.
- Es sagt es
auch Pindaros und viele andere Dichter, welche göttlicher Art sind.
- Und was sie
sagen, ist folgendes – erwäge aber wohl, ob dich dünkt, daß
sie wahr reden –:
phasi gar tên psuchên tou anthrôpou einai athanaton,
- kai tote men
teleutan – ho dê apothnêiskein kalousi -
- tote de palin
gignesthai, apollusthai d' oudepote:
Sie sagen nämlich, die Seele des Menschen sei unsterblich,
- so daß
sie zu einer Zeit zwar ende, was man Sterben nennt,
- zu anderer
Zeit jedoch wieder werde, untergehe aber niemals.
dein dê dia tauta hôs hosiôtata diabiônai ton bion:
- oisin gar
an –
Und deshalb müsse man aufs heiligste sein Leben verbringen.
- Denn von welchen
- Phersephona
poinan palaiou pentheos
- dexetai, eis
ton huperthen alion keinôn enatôi etei
- andidoi psuchas
palin,
- [81c] ek tan
basilêes agauoi
- kai sthenei
kraipnoi sophiai te megistoi
- andres auxont',
es de ton loipon chronon hêrôes agnoi
- pros anthrôpôn
kaleuntai.
"Persephone schon die Strafen des alten Elends
- genommen,
deren Seelen gibt sie der obern Sonne
- im neunten
Jahre zurück,
- (c) aus welchen
dann ruhmvolle tatenreiche
- Könige
und an Weisheit die vorzüglichsten
- Männer
hervorgehn, und von da an als heilige Heroen
- unter den
Menschen genannt werden.
[15. Überwindung des Einwands durch die Lehre der Wiedererinnerung]
hate oun hê psuchê athanatos te ousa kai pollakis gegonuia,
- kai eôrakuia
kai ta enthade kai ta en Haidou kai panta chrêmata,
hôste ouden thaumaston kai peri aretês kai peri allôn hoion t' einai
- autên
anamnêsthênai, ha ge kai proteron êpistato.
Weil nun die Seele unsterblich ist und oftmals geboren
- und, was hier
ist und in der Unterwelt, alles erblickt hat:
so daß nicht zu verwundem ist, wenn sie auch von der Tugend und allem andern vermag,
- sich dessen
zu erinnern, was sie ja auch früher gewußt hat.
ouden kôluei en monon anamnêsthenta-
- - ho
dê mathêsin kalousin anthrôpoi –
- - t'alla
panta auton aneurein, ean tis andreios êi kai mê
apokamnêi zêtôn:
Denn da die ganze (d) Natur unter sich verwandt ist und die Seele alles innegehabt hat:
so hindert nichts, daß, wer nur an ein einziges erinnert wird,
- was bei den
Menschen Lernen heißt,
- alles übrige
selbst auffinde, wenn er nur tapfer ist und nicht ermüdet im Suchen.
oukoun dei peithesthai toutôi tôi eristikôi logôi:
- houtos men
gar an hêmas argous poiêseien
- kai estin
tois malakois tôn anthrôpôn hêdus akousai,
- hôi
egô pisteuôn alêthei einai
- ethelô
meta sou zêtein aretê hoti estin.
Keineswegs also darf man jenem streitsüchtigen Satze folgen;
- denn er würde
uns träge machen
- und ist nur
den weichlichen Menschen angenehm zu hören;
- welchem vertrauend,
daß er wahr sei,
- ich eben Lust
habe, mit dir zu untersuchen, was die Tugend ist.
MEN. nai, ô Sôkrates: alla pôs legeis touto, hoti ou manthanomen,
- alla hên
kaloumen mathêsin anamnêsis estin?
Menon: Ja, Sokrates, aber meinst du dies so schlechthin, daß wir nicht lernen,
- sondern daß,
was wir so nennen, nur ein Erinnern ist?
SÔ. kai arti eipon, ô Menôn, hoti panourgos ei,
kai [82a] nun erôtais ei echô se didaxai,
- hos ou phêmi
didachên einai all' anamnêsin,
- hina dê
euthus phainômai autos emautôi t'anantia legôn.
Sokrates: Schon eben sagte ich, daß du schlau bist, Menon;
auch (82 a) jetzt fragst du, ob ich dich lehren kann,
- der ich doch
behaupte, es gebe keine Belehrung, sondern nur Erinnerung,
- damit ich
nur gleich mit mir selbst im Widerspruch erscheine.
MEN. ou ma ton Dia, ô Sôkrates, ou pros touto blepsas eipon, all' hupo tou ethous.
- all' ei pôs
moi echeis endeixasthai hoti echei hôsper legeis, endeixai.
Menon: Nein wahrlich, Sokrates, nicht in solcher Absicht sagte ich es, sondern aus Gewohnheit.
- Wenn du mir
also irgendwie zeigen kannst, daß es sich so verhält, wie du
sagst, so tue es.
SÔ. all' esti men ou raidion, homôs de ethelô prothumêthênai sou heneka.
alla moi proskaleson tôn pollôn [82b] akolouthôn toutôni tôn sautou hena, hontina boulei,
- hina en toutôi
soi epideixômai.
Sokrates: Freilich ist dies nicht leicht, ich will es aber doch unternehmen, dir zuliebe.
Rufe mir also von den vielen Dienern hier, (b) welche dich begleiten, irgendeinen her, welchen du willst,
- damit ich
es dir an diesem zeige.
MEN. panu ge. deuro proselthe.
Menon: Sehr gern. Du da, komm her.
SÔ. Hellên men esti kai hellênizei?
Sokrates: Er ist doch ein Hellene und spricht hellenisch?
MEN. panu ge sphodra, oikogenês ge.
Menon: Sehr gut; er ist im Hause aufgezogen.
SÔ. proseche dê ton noun hopoter' an soi phainêtai,
- ê anamimnêiskomenos
ê manthanôn par' emou.
Sokrates: Merke also wohl auf, wie er dir erscheinen wird,
- ob, als erinnerte
er sich oder als lernte er von nur.
MEN. alla proshexô.
Menon: Das will ich tun.
[16. Beweis dieser Lehre durch Befragung eines Sklaven]
SÔ. eipe dê moi, ô pai, gignôskeis tetragônon chôrion hoti toiouton estin?
Sokrates: Sage mir also, Knabe, weißt du wohl, daß ein Viereck eine solche Figur ist?
PAIS egôge.
Knabe: Das weiß ich.
SÔ. estin
oun [82c] tetragônon chôrion isas echon tas grammas tautas
pasas, tettaras ousas?
(c) Sokrates:
Gibt es also ein Viereck, welches alle diese Seiten, deren vier sind, gleich
hat?
PAIS panu
ge.
Knabe: Allerdings.
SÔ.
ou kai tautasi tas dia mesou estin isas echon?
Sokrates:
Hat es nicht auch diese beiden, welche durch die Mitte hindurchgehen, gleich?
PAIS nai.
Knabe: Ja.
SÔ.
oukoun eiê an toiouton chôrion kai meizon kai elatton?
Sokrates:
Ein solcher Raum nun kann doch größer und kleiner sein.
PAIS panu
ge.
Knabe: Freilich.
SÔ. ei oun eiê autê hê pleura duoin podoin kai autê duoin,
- posôn
an eiê podôn to holon?
- allo ti hapax
an ên duoin podoin to chôrion?
Sokrates: Wenn nun diese Seite zwei Fuß hätte und diese auch zwei;
- wieviel Fuß
enthielte das Ganze? –
- enthielte
dann nicht der ganze Raum einmal zwei Fuß?
PAIS [82d] nai.
Knabe: Ja.
SÔ. epeidê de duoin podoin kai tautêi,
- allo ti ê
dis duoin gignetai?
- wird er nicht
(d) von zweimal zwei Fuß?
PAIS gignetai.
Knabe: Das wird er.
SÔ. duoin ara dis gignetai podôn?
Sokrates: Zweimal zwei Fuß ist er also?
PAIS nai.
Knabe: Ja.
SÔ. posoi oun eisin hoi duo dis podes? logisamenos eipe.
Sokrates: Wieviel nun zweimal zwei Fuß sind, das rechne aus und sage es.
PAIS tettares, ô Sôkrates.
Knabe: Vier, o Sokrates.
SÔ. oukoun genoit' an toutou tou chôriou heteron diplasion,
- toiouton de,
isas echon pasas tas grammas hôsper touto?
Sokrates: Kann es nun nicht einen andern Raum geben, der das doppelte von diesem wäre,
- sonst aber
ein ebensolcher, in dem alle Seiten gleich sind, wie in diesem?
PAIS nai.
Knabe: O ja.
SÔ. posôn
oun estai podôn?
Sokrates:
Wieviel Fuß muß er enthalten?
PAIS oktô.
Knabe: Acht
Fuß.
SÔ.
phere dê, peirô moi eipein pêlikê tis estai [82e]
ekeinou hê grammê hekastê.
- hê men
gar toude duoin podoin:
Sokrates: Gut! Nun versuche auch, mir zu sagen, wie groß jede Seite in diesem Viereck sein wird.
- Nämlich
die des ersten ist von zwei Fuß?
PAIS dêlon dê, ô Sôkrates, hoti diplasia.
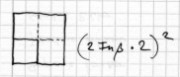
Knabe: Offenbar, o Sokrates, zweimal so groß.
SÔ. horais, ô Menôn, hôs egô touton ouden didaskô, all' erôtô panta?
kai nun houtos oietai eidenai hopoia estin aph' hês to oktôpoun chôrion genêsetai:
- ê ou
dokei soi?
Sokrates: Siehst du wohl, Menon, wie ich diesen nichts lehre, sondern alles nur frage?
Und jetzt glaubt er zu wissen, wie groß die Seite ist, aus der das achtfüßige Viereck entstehen wird.
- Oder denkst
du nicht, daß er es glaubt?
MEN. emoige.
Menon: Allerdings.
SÔ. oiden oun?
Sokrates: Weiß er es aber wohl?
MEN. ou dêta.
Menon: Wohl nicht.
SÔ. oietai de ge apo tês diplasias?
Sokrates: Er glaubt aber doch, es entstehe aus der doppelten?
MEN. nai.
Menon: Ja.
[17. Dessen unvollkommene Lösungsversuche des geometrischen Problems]
SÔ. theô dê auton anamimnêiskomenon ephexês, hôs dei anamimnêiskesthai.
su de moi lege: apo tês diplasias grammês phêis to [83a] diplasion chôrion gignesthai?
- toionde legô,
mê tautêi men makron, têi de brachu,
- alla ison
pantachêi estô hôsper touti,
- diplasion
de toutou, oktôpoun:
Sokrates: Sieh nun zu, wie er sich weiter so erinnern wird, wie man sich erinnern muß. –
Du aber sage mir, aus der doppelten Seite, sagst du, entstehe das doppelte Viereck?
- Ich meine
aber ein solches, (83 a) nicht etwa eins, das hier lang ist, dort aber
kurz;
- sondern es
soll nach allen Seiten gleich sein, wie dieses hier,
- aber das Zwiefache
von diesem, also achtfüßig.
PAIS emoige.
Knabe: So meine ich.
SÔ. oukoun diplasia autê tautês gignetai,
- an heteran
tosautên prosthômen enthende?
Sokrates: Wohl! Dies wird doch die zwiefache von dieser,
- wenn wir hier
noch eine ebenso große hinzusetzen?
PAIS panu ge.
Knabe: Allerdings.
SÔ. apo tautês dê, phêis, estai to oktôpoun chôrion,
- an tettares
tosautai [83b] genôntai?
Sokrates: Und aus dieser, glaubst du, werde das achtfüßige Viereck entstehen,
- wenn wir vier
solche nehmen?
PAIS nai.
Knabe: Ja. (b)
SÔ. anagrapsômetha dê ap' autês isas tettaras.
- allo ti ê
touti an eiê ho phêis to oktôpoun einai?
Sokrates: So laß uns von ihr vier gleiche aufzeichnen.
- Nicht wahr
also, dies wäre, was du für das achtfüßige hältst?
PAIS panu ge.
Knabe: Allerdings.
SÔ.
oukoun en autôi estin tauti tettara,
- hôn
hekaston ison toutôi estin tôi tetrapodi?
Sokrates: Sind nun nicht in ihm diese vier,
- deren jedes
diesem Vierfüßigen gleich ist?

PAIS nai.
Knabe:: Ja.
SÔ. poson oun gignetai? ou tetrakis tosouton;
Sokrates: Wie groß ist es also? Nicht viermal so groß?
PAIS pôs d' ou?
Knabe: Nicht anders.
SÔ. diplasion oun estin to tetrakis tosouton?
Sokrates: Ist nun das viermal so große das zwiefache?
PAIS ou ma Dia.
Knabe: Nein, beim Zeus.
SÔ. alla posaplasion?
Sokrates: Sondern das wievielfache?

PAIS tetraplasion.
Knabe: Das vierfache.
SÔ. apo tês diplasias [83c] ara, ô pai, ou diplasion alla tetraplasion gignetai chôrion.
Sokrates: Aus der zwiefachen Seite also entsteht uns nicht das (c) zwiefache, sondern das vierfache Viereck.
PAIS alêthê legeis.
Knabe: Du hast recht.
SÔ. tettarôn gar tetrakis estin hekkaideka. ouchi?
Sokrates: Denn von vier ist das Vierfache sechzehn. Nicht?
PAIS nai.
Knabe: Ja.
SÔ. oktôpoun d' apo poias grammês?
- ouchi apo
men tautês tetraplasion?
Sokrates: Das achtfüßige aber, von welcher Seite entsteht das?
- Nicht wahr,
aus dieser entsteht das vierfache?
PAIS phêmi.
Knabe: Das sage ich auch.
SÔ. tetrapoun de apo tês hêmiseas tautêsi touti?
Sokrates: Und das vierfüßige entsteht aus dieser halben?
PAIS nai.
Knabe: Ja.
SÔ. eien: to de oktôpoun ou toude men diplasion estin,
- toutou de
hêmisu?
Sokrates: Wohl. Das achtfüßige aber, ist es nicht von diesem hier das Zwiefache,
- von diesem
aber die Hälfte?
< PAIS nai.>
Knabe: Allerdings.
SÔ. ouk apo men meizonos estai ê tosautês grammês,
- apo elattonos
de ê [83d] tosêsdi; ê ou?
Sokrates: Muß es also nicht aus einer größeren Seite entstehen als diese
- und aus einer
kleineren als diese? Oder nicht?
PAIS emoige dokei houtô.
(d) Knabe: Ich wenigstens denke so.
SÔ. kalôs:
- to gar soi
dokoun touto apokrinou.
Sokrates: Schön!
- Denn immer
nur, was du denkst, mußt du antworten.
PAIS nai.
Knabe: Ja.
SÔ. dei ara tên tou oktôpodos chôriou grammên meizô men einai têsde tês dipodos,
- elattô
de tês tetrapodos.
Sokrates: Also muß des achtfüßigen Viereckes Seite größer sein als diese zweifüßige
- und kleiner
als die vierfüßige?
PAIS dei.
Knabe: Das muß sie.
[83e] SÔ. peirô dê legein pêlikên tina phêis autên einai.
(e) Sokrates: So versuche denn zu sagen, wie groß du meinst, daß sie sei.
PAIS tripoda.

Knabe: Dreifüßig.
SÔ. oukoun hanper tripous êi,
- to hêmisu
tautês proslêpsometha kai estai tripous?
- kai enthende
hôsautôs duo men oide, ho de eis.
Sokrates: Gut. Wenn sie dreifüßig sein soll,
- so wollen
wir von dieser noch die Hälfte dazunehmen, so wird sie dreifüßig;
- und auf dieser
Seite ebenso sind dies zwei, dies einer.
PAIS nai.
Knabe: Ja.
SÔ. oukoun an êi têide triôn kai têide triôn,
- to holon chôrion
triôn tris podôn gignetai?
Sokrates: Wenn es nun hier drei Fuß hat und hier auch drei Fuß:
- so wird das
ganze Viereck von dreimal drei Fuß.
PAIS phainetai.
Knabe: Offenbar.
SÔ. treis de tris posoi eisi podes?
Sokrates: Dreimal drei aber, wieviel Fuß sind das?

PAIS ennea.
Knabe: Neun.
SÔ. edei de to diplasion posôn einai podôn?
Sokrates: Wieviel Fuß aber sollte das zwiefache enthalten?
PAIS oktô.
Knabe: Acht.
SÔ. oud' ar' apo tês tripodos pô to oktôpoun chôrion gignetai.
Sokrates: Auch nicht aus der dreifüßigen Seite also wird uns das achtfüßige Viereck.
PAIS ou dêta.
Knabe: Freilich nicht.
SÔ. all' apo poias; peirô hêmin eipein akribôs:
- kai [84a]
ei mê boulei arithmein, alla deixon apo poias.
Sokrates: Von welcher also, das versuche doch uns genau zu bestimmen;
- und wenn du
es nicht durch Zählen willst, so zeige uns (84 a) nur, von welcher.
PAIS alla ma ton Dia, ô Sôkrates, egôge ouk oida.
Knabe: Aber beim Zeus, Sokrates, ich weiß es nicht.
[18. Nutzen der im Sklaven erzeugten Verwirrung]
SÔ. ennoeis au, ô Menôn, hou estin êdê badizôn hode tou anamimnêiskesthai?
hoti to men prôton êidei men ou, hêtis estin hê tou oktôpodos chôriou grammê,
- hôsper
oude nun pô oiden,
- kai ouch hêgeito
aporein:
- kai hôsper
ouk oiden, oud' oietai eidenai.
Sokrates: Siehst du wohl, Menon, wie weit er schon fortgeht im Erinnern?
Denn zuerst wußte er zwar auch keineswegs, welches die Seite des achtfüßigen Vierecks ist,
- wie er es
auch jetzt noch nicht weiß:
- und glaubte
nicht, in Verlegenheit zu kommen.
- und wie er
es nicht weiß, so glaubt er es auch nicht zu wissen. (b)
MEN. alêthê legeis.
Menon:Du hast recht.
SÔ. oukoun nun beltion echei peri to pragma ho ouk êidei?
Sokrates: Steht es also nun nicht besser mit ihm in Bezug auf die Sache, die er nicht wüßte?
MEN. kai touto moi dokei.
Menon: Auch das dünkt mich.
SÔ. aporein oun auton poiêsantes kai narkan hôsper hê narkê,
- môn
ti eblapsamen?
Sokrates: Indem wir ihn also in Verlegenheit brachten und zum Erstarren, wie der Zitterrochen,
- haben wir
ihm dadurch etwa Schaden getan?
MEN. ouk emoige dokei.
Menon: Mich dünkt nicht.
SÔ. prourgou goun ti pepoiêkamen, hôs eoike,
- pros to exeurein
hopêi echei:
tote de raidiôs an kai pros pollous kai pollakis [84c] ôiet' an
- eu legein
peri tou diplasiou chôriou,
- hôs
dei diplasian tên grammên echein mêkei.
Sokrates: Vielmehr haben wir vorläufig etwas ausgerichtet, wie es scheint,
- damit er herausfinden
kann, wie sich die Sache verhält.
damals aber glaubte er, ohne Schwierigkeit vor vielen oftmals
- gut zu reden
über das zwiefache Viereck,
- daß
es auch eine zwiefach so lange (c) Seite haben müsse.
MEN. eoiken.
Menon: So mag es wohl sein.
SÔ. oiei oun an auton proteron epicheirêsai zêtein ê manthanein touto
- ho ôieto
eidenai ouk eidôs,
- prin eis aporian
katepesen hêgêsamenos mê eidenai,
- kai epothêsen
to eidenai?
Sokrates: Glaubst du nun, er würde sich vorher bemüht haben, das zu suchen oder zu lernen,
- was er nichtwissend
glaubte zu wissen,
- ehe er, überzeugt,
er wisse nicht, in Verwirrung geriet
- und sich nach
dem Wissen sehnte?
MEN. ou moi dokei, ô Sôkrates.
Menon: Nein, dünkt mich, Sokrates.
SÔ. ônêto ara narkêsas?
Sokrates: Nutzen hat ihm also das Erstarren gebracht?
MEN. dokei moi.
Menon: So dünkt mich.
SÔ. skepsai dê ek tautês tês aporias hoti kai aneurêsei zêtôn met' emou,
- ouden all'
ê erôtôntos emou kai ou didaskontos:
- alla mê
tas toutou doxas anerôtônta.
Sokrates: Sieh nun aber auch zu, was er von dieser Verlegenheit aus mit mir suchend auch finden wird,
- indem ich
ihn immer nur frage und niemals lehre.
- und nicht
seine eigenen Gedanken nur ihm abfrage.
[19. Sein Finden der Lösung]
lege gar moi su: ou to men tetrapoun touto hêmin esti chôrion; manthaneis?
Sage mir du, ist dies nicht unser vierfüßiges Viereck? Verstehst du?
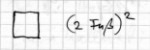
PAIS egôge.
Knabe: Ja.
SÔ. heteron de autôi prostheimen an touti ison?
Sokrates: Können wir nun nicht hier noch ein gleiches daran setzen?
PAIS nai.
Knabe: Ja.
SÔ. kai triton tode ison hekaterôi toutôn?
Sokrates: Und auch dies dritte, das jedem von den beiden gleich ist?
PAIS nai.
Knabe: Ja.
SÔ. oukoun prosanaplêrôsaimeth' an to en têi gôniai tode?
Sokrates: Können wir nun nicht auch das noch hier in der Ecke ausfüllen?

PAIS panu ge.
Knabe: Allerdings.
SÔ. allo ti oun genoit' an tettara isa chôria [84e] tade?
Sokrates: Sind dies nun nicht vier gleiche (e) Vierecke?
PAIS nai.
Knabe: Ja.
SÔ. ti oun; to holon tode posaplasion toude gignetai?
Sokrates: Wie nun? Das wievielfache ist wohl dies Ganze von diesen?
PAIS tetraplasion.
Knabe: Das vierfache.
SÔ. edei de ge diplasion hêmin genesthai: ê ou memnêsai?
Sokrates: Wir sollten aber ein zweifaches bekommen; oder erinnerst du dich nicht?
PAIS panu ge.
Knabe: Allerdings.
SÔ. oukoun estin autê grammê ek gônias eis gônian [85a]
- [tina] temnousa
dicha hekaston toutôn tôn chôriôn?
Sokrates: Schneidet nun nicht diese Linie, welche aus einem Winkel in den anderen geht (85 a),
- jedes von
diesen Vierecken in zwei gleiche Teile?
PAIS nai.
Knabe: Ja.
SÔ. oukoun tettares autai gignontai grammai isai, periechousai touti to chôrion?
Sokrates: Und werden nicht dieses vier gleiche Linien, welche dieses Viereck einschließen?
PAIS gignontai gar.
Knabe: Allerdings.
SÔ. skopei dê: pêlikon ti estin touto to chôrion?
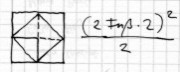
Sokrates: So betrachte nun, wie groß wohl dieses Viereck ist?
PAIS ou manthanô.
Knabe: Das verstehe ich nicht.
SÔ. ouchi tettarôn ontôn toutôn hêmisu hekastou hekasth hê grammê apotetmêken entos?
- ê ou;
Sokrates: Hat nicht von diesen vieren von je einem jede Seite die Hälfte nach innen zu abgeschnitten?
- Oder nicht?
PAIS nai.
Knabe: Ja.
SÔ. posa oun têlikauta en toutôi enestin?
Sokrates: Wieviel solche sind nun in diesem?
PAIS tettara.
Knabe: Vier.
SÔ. posa de en tôide?
Sokrates: Wieviel aber in diesem?
PAIS duo.
Knabe: Zwei.
SÔ. ta de tettara toin duoin ti estin?
Sokrates: Vier aber ist von zwei was doch?
PAIS diplasia.
Knabe: Das Zweifache.
SÔ. tode oun [85b] posapoun gignetai?
Sokrates: Wievielfüßig (b) ist also dieses?

PAIS oktôpoun.
Knabe: Achtfüßig.
SÔ. apo poias grammês?
Sokrates: Von welcher Linie?
PAIS apo tautês.
Knabe: Von dieser.
SÔ. apo tês ek gônias eis gônian teinousês tou tetrapodos?
Sokrates: Von der, welche aus einem Winkel in den andern das vierfüßige schneidet?
PAIS nai.
Knabe: Ja.
SÔ. kalousin de ge tautên diametron hoi sophistai:
- hôst'
ei tautêi diametros onoma,
- apo tês
diametrou an, hôs su phêis, ô pai Menônos,
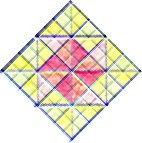
- gignoit' an
to diplasion chôrion.
Sokrates: Diese nun nennen die Gelehrten die Diagonale;
- so daß,
wenn diese die Diagonale heißt,
- alsdann aus
der Diagonale, wie du behauptest,
- das zwiefache
Viereck entsteht.
PAIS panu men oun, ô Sôkrates.
Knabe: Allerdings, Sokrates.
[20. Folgerung: Der Ursprung der Erkenntnis liegt im Lernenden selbst]
SÔ. ti soi dokei, ô Menôn?
- estin hêntina
doxan ouch autou houtos apekrinato?
Sokrates: Was dünkt dich nun, Menon?
- Hat dieser
irgendeine Vorstellung, die nicht sein war, zur Antwort gegeben?
[85c] MEN. ouk, all' heautou.
(c) Menon: Nein, nur seine eignen.
SÔ. kai mên ouk êidei ge, hôs ephamen oligon proteron.
Sokrates: Und doch wußte er es vor kurzem noch nicht wie wir gestanden?
MEN. alêthê legeis.
Menon: Ganz recht.
SÔ. enêsan de ge autôi hautai hai doxai: ê ou?
Sokrates: Es waren aber doch diese Vorstellungen in ihm. Oder nicht?
MEN. nai.
Menon: Ja.
SÔ. tôi ouk eidoti ara peri hôn an mê eidêi eneisin alêtheis doxai peri toutôn hôn ouk oide?
Sokrates: In dem Nichtwissenden also sind von dem, was er nicht weiß, dennoch richtige Vorstellungen.
MEN. phainetai.
Menon: Das zeigt sich.
SÔ. kai
nun men ge autôi hôsper onar arti anakekinêntai
hai doxai autai:
ei de auton
tis anerêsetai pollakis ta auta tauta kai pollachêi,
- oisth' hoti
teleutôn oudenos hêtton akribôs
- [85d] epistêsetai
peri toutôn.
Sokrates: Und jetzt sind ihm nur wie im Traume diese Vorstellungen eben aufgeregt.
Wenn ihn aber jemand oftmals um dies nämliche befragt und auf vielfache Art:
- so wisse nur,
daß er am Ende nicht minder genau als irgendein anderer
- um diese Dinge
wissen (d) wird.
MEN. eoiken.
Menon: Das scheint wohl.
SÔ. oukoun oudenos didaxantos all' erôtêsantos
- epistêsetai,
analabôn autos ex autou tên epistêmên?
Sokrates: Indem ihn also niemand belehrt, sondern nur ausfragt,
- wird er wissen
und wird die Erkenntnis nur aus sich selbst hervorgeholt haben?
MEN. nai.
Menon: Ja.
SÔ. to de analambanein auton en autôi epistêmên ouk anamimnêiskesthai estin?
Sokrates: Dieses nun, selbst aus sich eine Erkennmis hervorholen, heißt das nicht sich erinnern?
MEN. panu ge.
Menon: Allerdings.
SÔ. ar' oun ou tên epistêmên, hên nun houtos echei,
- êtoi
elaben pote ê aei eichen?
Sokrates: Und hat etwa nicht dieser die Erkennmis, die er jetzt hat,
- entweder einmal
erlangt oder immer gehabt?
MEN. nai.
Menon: Ja.
SÔ. oukoun ei men aei eichen, aei kai ên epistêmôn:
- ei de elaben
pote, ouk an en ge tôi nun biôi eilêphôs
eiê.
Sokrates: Hat er sie nun immer gehabt, so ist er auch immer wissend gewesen.
- Hat er sie
aber einmal erlangt, so hat er sie wenigstens nicht in diesem Leben erlangt.
ê [85e] dedidachen tis touton geômetrein?
houtos gar poiêsei peri pasês geômetrias t'auta tauta,
- kai tôn
allôn mathêmatôn hapantôn.
- dikaios gar
pou ei eidenai, allôs te epeidê en têi sêi
oikiai gegonen kai tethraptai.
Oder hat jemand diesen die Geometrie gelehrt?
Denn gewiß wird er mit der ganzen Geometrie (e) ebenso verfahren
- und mit allen
andern Wissenschaften auch.
- Denn du mußt
es ja wohl wissen, da er in deinem Hause geboren und erzogen ist.
MEN. all' oida egôge hoti oudeis pôpote edidaxen.
Menon: Ich weiß sehr gut, daß niemand sie ihn jemals gelehrt hat.
SÔ. echei de tautas tas doxas, ê ouchi?
Sokrates: Er hat aber diese Vorstellungen; oder nicht?
MEN. anankê, ô Sôkrates, phainetai.
Menon: Notwendig, wie man ja sieht
[21. Rückschluß daraus auf die Unsterblichkeit]
SÔ. ei de mê en tôi nun biôi labôn,
- ouk êdê
touto [86a] dêlon, hoti en allôi tini chronôi
eiche kai ememathêkei?
Sokrates: Wenn er sie aber in diesem Leben nicht erlangt hat und daher nicht wußte:
- so hat er
sie ja offenbar in einer andern Zeit gehabt und gelernt. (86a)
MEN. phainetai.
Menon: Offenbar.
SÔ. oukoun houtos ge estin ho chronos hot' ouk ên anthrôpos;
Sokrates: Ist nun nicht dieses die Zeit, wo er kein Mensch war?
MEN. nai.
Menon: Offenbar.
SÔ. ei oun hon t' an êi chronon kai hon an mê êi anthrôpos,
- enesontai
autôi alêtheis doxai,
- hai erôtêsei
epegertheisai epistêmai gignontai,
- dêlon
gar hoti ton panta chronon estin ê ouk estin anthrôpos.
Sokrates: Wenn also in der ganzen Zeit, wo der Mensch ist, oder auch, wo er es nicht ist,
- richtige Vorstellungen
in ihm sein sollen,
- welche, durch
Fragen aufgeregt, Erkenntnisse werden,
- Denn offenbar
ist er durch alle Zeit entweder Mensch oder nicht.
MEN. phainetai.
Menon: Das ist einleuchtend.
[86b] SÔ. oukoun ei aei hê alêtheia hêmin tôn ontôn estin en têi psuchêi,
- athanatos
an hê psuchê eiê,
- –
touto d' estin ho mê memnêmenos
–
- epicheirein
zêtein kai anamimnêiskesthai?
Sokrates: Wenn nun von jeher immer die Wahrheit von allem, (b) was ist, der Seele einwohnt,
- so wäre
ja die Seele unsterblich,
- das heißt
aber, dessen du dich nicht erinnerst,
- trachten kannst
zu suchen und dir zurückzurufen.
MEN. eu moi dokeis legein, ô Sôkrates, ouk oid' hopôs.
Menon: Du scheinst mir, ich weiß nicht wie, vortrefflich zu reden, Sokrates.
SÔ. kai gar egô emoi, ô Menôn.
- kai ta men
ge alla ouk an panu huper tou logou diischurisaimên:
- beltious an
eimen kai andrikôteroi kai hêtton argoi
- mêde
dein zêtein,
Sokrates: Auch mir selbst scheine ich es, o Menon.
- Und das Übrige
freilich möchte ich nicht eben ganz verfechten für diese Rede;
- besser werden
und mannhafter und weniger träge, (c)
- und man müsse
es also auch nicht erst suchen,
MEN. kai touto men ge dokeis moi eu legein, ô Sôkrates.
Menon: Auch dies dünkt mich sehr richtig gesagt, Sokrates.
SÔ. boulei oun, epeidê homonooumen hoti zêthteon peri hou mê tis oiden,
- epicheirêsômen
koinêi zêtein ti pot' estin aretê?
Sokrates: Da wir nun einig darüber sind, daß gesucht werden was jemand noch nicht weiß:
- willst du,
daß wir miteinander unternehmen zu suchen, was wohl die Tugend ist?